Cálculo diferencial na agricultura

Você se lembra ainda de cálculo diferencial e integral aprendido nas aulas de engenharia?

Já se perguntou onde poderíamos aplicar estes conceitos no nosso dia a dia? Eu já, mas se pensarmos com mais calma podemos ter uma visão diferente. Nas máquinas em geral foram desenvolvidas no auxílio do homem para executar suas tarefas, durante seu trabalho, executam movimentos mecânicos de várias formas.

Vamos abordar aqui um exemplo simples da mecânica clássica aplicando os conceitos de Cálculo diferencial, mais precisamente, taxas relacionadas. O problemas aqui poderia ser resolvido utilizando de conceitos da Dinâmica. Vejamos um exemplo de um pulverizador, ele possui barras articuladas movimentadas por auxílio de um atuador hidráulico que por sua vez é acionado por um fluxo de um fluido gerado por uma bomba hidráulica.

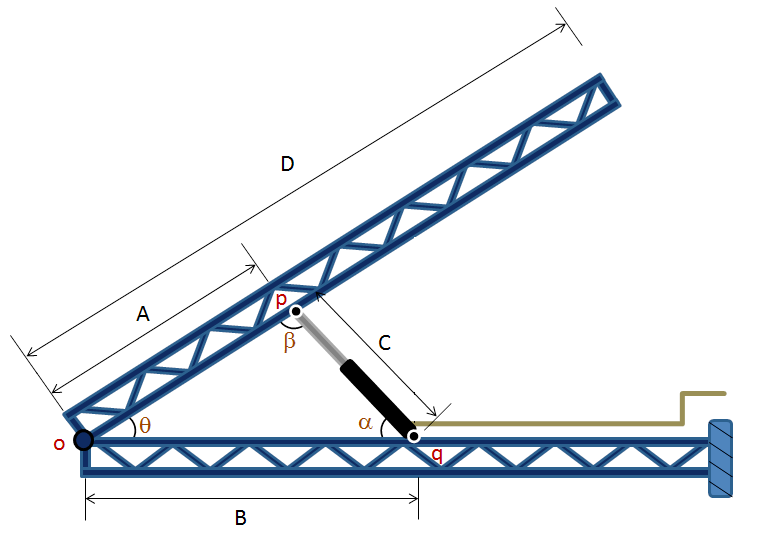
Se a bomba hidráulica gera um fluxo de óleo para o cilindro hidráulico expandindo a uma velocidade constante que consequentemente empurrará a barra para abertura então qual será a velocidade tangencial na ponta da barra quando o cilindro estiver com uma determinada abertura ou a um determinado ângulo. Fácil de se calcular? Vamos para os dados da figura abaixo:

• Fluxo de óleo = 125 x 10³ mm³/segundo;
• Área do êmbolo do cilindro hidráulico = 2500 mm²;
• Distância fixa “A” = 300 mm;
• Distância fixa “B” = 900 mm;
• Distância fixa “D” = 6000 mm;

Perguntando novamente, qual é a velocidade tangencial da ponta da barra quando o cilindro hidráulico “C” estiver com abertura de 700 mm?

Primeiramente descobriremos a taxa de abertura do cilindro:

Volume do cilindro V = A x h

[dV/dt] = A.[dh/dt]

[dh/dt] = [dV/dt] /(A)

[dh/dt] = (125 x 10³) / (2500) = 50 mm/s

A taxa de variação ou velocidade do cilindro é de 50 mm por segundo;

Aplicando a lei dos cossenos determinamos o ângulo θ:

C² = A² + B² – 2.A.B.(cos θ)

700² = 300² + 900² – 2*300*900*cos θ

θ = 40,6º

Aplicando derivada na coordenada polar determinamos a velocidade angular instantânea em θ  (40,6º):

C² = A² + B² – 2.A.B.(cos θ)

2.C.[dC/dt] = -2.A.B.(-sen θ). [dθ/dt]

2*700*[50] = 2*300*900*{sen (40,6º)}*[dθ/dt]

[dθ/dt] = 0,199 rad/s

Para finalizar determinamos a velocidade tangencial na ponta da barra:

Sabemos que o arco de uma circunferência é determinado pelo produto do raio e do ângulo em radianos e que a variação do arco é a própria velocidade tangencial, considerando raio como o comprimento “D” da barra:

Arco = R x θ

[dArco/dt] = R x [dθ/dt]

V = 6000 x 0,199

V = 1195,3 mm/s

Não foi a toa que Leibniz, Newton e outros filósofos, como eram denominados na época, desenvolveram a ferramenta matemática que tanto se aplica hoje na engenharia, física clássica, física moderna, economia, química e entre outros. Seria difícil calcular este tipo de problema sem os conceitos de Cálculo Diferencial, estudamos esta ferramenta para simplificar a nossa vida e não para complicar nos, exceto nos dias de prova, não é verdade? Você concorda?